かず(数)の教え方
1.子どもが「数をわかる」ということ

日本の家庭では、おふろで「十まで数えたら出ていいよ」というふうにして数を唱えさせることが多いのではないでしょうか。いまや幼稚園に入る前に百ぐらいまで言える子は珍しくないようです。でも
100までの数が言えたら100の数がわかっていると言えるのか
ということを、ちょっと考えていただきたいのです。
小さい子はよく「わたし、100までいえるよ!」と周りにあるコップや机や椅子を手当たり次第に指差して「いち、にぃ、さん、しぃ…」と数を言い続けたりします。ときどき言葉と指差しとがズレても平気。これってほんとうに数をわかっているのかな?
小さい子は、いくつかのコインを横一列に並べて、左から数えたときと右から数えたときの数が違っていても不思議に感じません。また、山盛りに積んだ石を数えるときに1回目と2回目の数がちがっていても平気な顔をして「1回目は△個、2回目は○個あった」と言ったりします。
「つけ加えたり取り除いたりしていないから、数は減ったり増えたりしない」
ということがまだ理解できていない段階です。
スイスの心理学者のピアジェ(Jean Piaget 1896~1980)が4~5歳の子を対象に実験を行っています。同数の花と花びんを用意して、花びんに花を1本ずつさしていきます。「花の数と花びんの数は同じですか?」と子ども達に聞くと「同じ」と答えます。だけど、花びんから花を抜いて一束にして同じ質問をすると「花びんが多い」と答える子がいます。さっきは同じ数だと言ったのに、寄せ集めて花の占める広さが変われば少なくなったと思ってしまうのです。
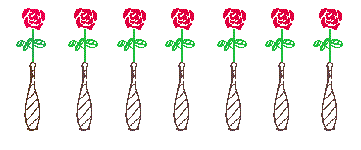
子どもはみな似たような過程を通って成長していくものです。
これが6歳くらいになると「同じ」とわかるようになるので、世界各国で義務教育が始まるのも6歳頃からになっているようです。つまり子どもは最初から「数」というものが脳の中にインプットされているかというと決してそうではない。そういう子どもたちにどうやって数を教えるのかというのが算数教育の目的になるわけです。
カラスのような動物も一から五までは識別できるという実験結果もあるそうです。
では人間の子どもが数がわかるようになるのはどんな内容が伴った時なのか。その道筋をたどってみることにしましょう。
2. なかまあつめ(集合づくり)
◎なかまあつめ(集合づくり)
もともと数は「ものの集まりの大きさ」を表すために考え出されました。
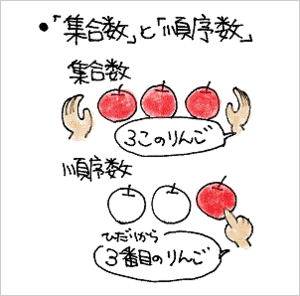
リンゴが2こ、スプーンが3本、犬が4ひき、人が5人という個数を表す数を「集合数」と言います。
いっぽうで、「2番目」「5列目」「1丁目」などの順番を表す数を「順序数」と言い、区別しています。
集合数は自由にたしざんひきざんができますが、順序数は、たとえば、1等賞と3等賞をたしても4等賞にはならないように自由にたしざんひきざんができません。
子どもには、最も根源的な数、「集合数」から教えます。
この時に問題なのは、「何を数えるのか」ということです。リンゴもコップも犬も人も手当たり次第に数えてしまっては何の数だかわかりません。
そこでまずはじめに「仲間あつめ(仲間はずれ)」をしていきます。子どもたちになじみのあるもので同じ種類のものと違う種類のものとに分けられるかどうか、集合づくりをします。
「仲間=同じものの集まり(=集合)」

◎大きい・小さい・同じ
3歳くらいになれば大きさの違うケーキなら大きい方を選びますので、大小の比較はある程度できるようになっています。
そこで量に関することばを学習していきます。
*大きいー小さい *長いー短い *高いー低い *多いー少ない *重い―軽い *広いーせまい
*浅いー深い *厚いー薄い ・・・などなど。
そして *〔同じ〕 についても学びます。
幼児期は遊びや生活そのものが『量の世界』です。
散歩、水遊び、砂遊び、どんぐりひろい、お絵かき、絵本・・・
「こっちの木には葉っぱが多いね。」
「高い鉄棒と低い鉄棒があるよ。」
「浅いプールで泳ごうか。」
幼児期には様々な体験をとおして「ことば」を獲得していきます。
量に対するイメージを広げていく時期を大事にしてあげたいものです。
3. 1対1対応
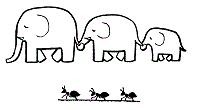
大きなゾウ1頭でも、小さなアリ1ぴきでも、一つ一つ分かれているものはみな「1」ですね。
ゾウ3頭とアリ3びきを1対1に対応させていけば余りが出ず同じ「3」ということになりま す。数は、色や形・大きさなどに関係なく個体数を考えます。
大昔、まだ人間が数をしらなかった時、「どちらが多いか、同じか」を1対1対応によって判断していたことがわかっています。
1対1対応というのは、例えば、コーヒーカップとお皿はどちらが多いか知りたければ、お皿にコーヒーカップをのせていき、最後に余りの出た方が多いことがわかります。そしてもし余りが出なければどちらも同じということになります。
初めは実物や絵カルタ(下の写真)などを手で動かして対応させると良いですよ。

鉛筆とキャップ、卵と卵入れ、ローソクとローソク立て、犬と首輪、子どもと帽子、などなど、1対1対応はいろいろ考えられます。
運動会の玉入れ競争で赤玉と白玉をかごの中から同時に放り投げてどちらが多いかを比べるのもそうですね。
この1対1対応の操作は、数を学ぶ上でとても大事ですから、「なかまあつめ」を学んだ後、数を導入する前に学習します。
子どもたちには、例えば夕食時に1人に1つずつスプーンを置くとか、お人形に1個ずつキャンディーをあげるというような場面を作ってあげるといいですよ。小さい子は手を使って物を並べたり置いたりする体験を重ねることで考える力を伸ばしていきます。
カップと皿のように自然に対応できる例だけではなく、スイカとさくらんぼのように大小が極端に違う物だとか、○と△といった抽象的な物どうしなど、いろいろな場面を考えて対応させていきます。
それから、並び方がきちんと整列していて分かりやすいときもあれば、バラバラに置かれたり詰まっていたりしてひと目でどちらが多いか分からないときなども取り入れます。1対1で線を結ぶとか、動かせる物は重ねてみるなどの操作をして多い少ないを調べていきます。
◎タイルとの1対1対応
数というのはとても抽象的でつかみにくいものです。
「3」といわれて子どもたちは頭の中で何をイメージすればよいでしょう。
リンゴやゾウといった具体的なものを思い浮かべていては混乱してしまいます。そこでリンゴやゾウといった具体物の代わりに正方形の「タイル」(□)を使います。いままでの物と物との1対1対応から、物とタイルの1対1対応も練習します。タイルをイチゴと同じ多さだけ置かせてみたり、二種類のものの多さをタイルを仲立ちにしてくらべさせたりします。
4. タイルが仲立ちに!
◎いよいよ「数」(集合数)へ
もしあなたが「どこかに3があったら持ってきて下さい」と言われたとしたら、持ってくることができますか?
世の中に存在する物は「鉛筆が3本」であり「ひとが3人」です。純粋な「3」はあるのか…見た人は誰もいません。
色々な事物の集まりを見ていくうちに〈3匹のさかな、3個の石ころ、3本の木〉などに共通な要素として「3」が生まれてきたということです。
大人にとってはなんでもない「数」も実は抽象的なもので、そこが、具体的な世界で生きている子どもたちには教えにくいところなのです。
そこで水道方式では、すべての「3」を代表する物として「タイル」(□)を使っていきます。
タイルは、時には3このりんごの代わりになるし、3人のひとの代わりにもなり、何の代わりにもなって数との間の仲立ちをしてくれます。
小学校に入るとおはじきなどを使って勉強しますが、タイルだと先々、小数や分数にまで使えるのです。
タイルは、数字と量の橋渡しをするという点で非常に優れています。
同時に、子どもが手でタイルを動かして勉強できるところがいいのです。
「数」の導入は、初めに「3」から教えて、次に「2」→「1」→「4」→「5」…という順で進めていきます。
かぶとむしもこおろぎも、そしてちょうちょも、タイル3個[□□□]と同じ数だけいます。
このタイルのかずが「3」です。
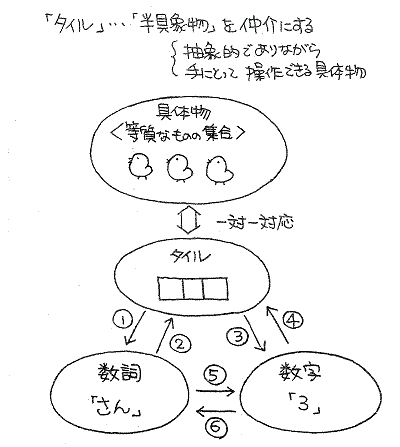
「タイル」と「数のことば(数詞)」と「数字」のそれぞれの関係がわかってすぐ答えられるように十分練習します。
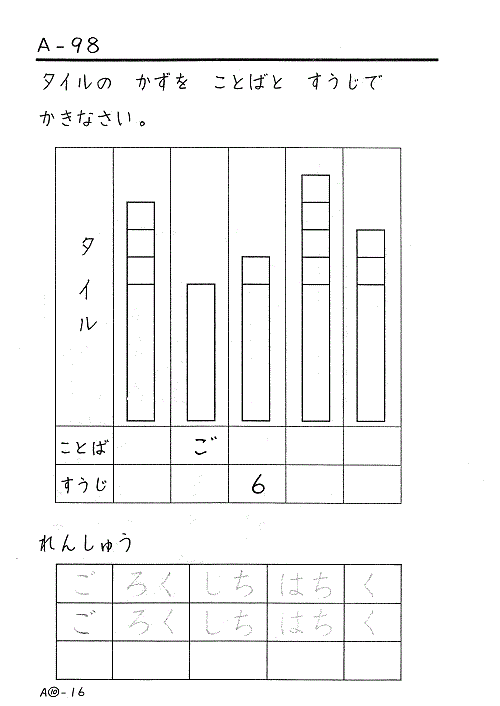
次の図の①~⑥のような順序で進めると良いでしょう。
※ 教え方のポイント!「0」を教えるなら・・・
「0」(れい)を教えるときは、「なんにもないのが0だよ」という説明だと子どもたちにはピンときません。
お皿にあった数枚のクッキーが食べられてなくなり、とうとうお皿だけになってしまった…というように、「あったものがなくなった」(入れ物だけが残っている)という場面を見せて「0」を説明してあげるとわかりやすいですよ。
◎「5」のタイル
「5」までを教えたら、ちびタイル(□)5個をつなげて「5のタイル」に代え、6以上の数を教えていきましょう。
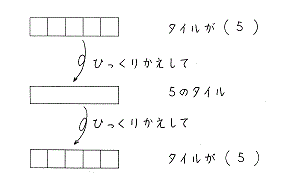
5のタイルとちびタイル1個で「6」に、5のタイルとちびタイル2個で「7」になります。5のタイルを使うことで6以上 の数も一目で分かります。

いちばんぼし算数数学教室さん制作の YouTube算数動画
↓
◎十進記数法とタイル
タイルが良いもう一つの理由は、「十進記数法(じっしんきすうほう)」がとてもよくわかることです。
私たちがふだん使っている数字は、十集まれば次の位に一くり上がります。「9」より1大きい数を「10」と書くのもそのためです。これによって0~9までの十個の数字だけでどんなに大きな数もどんなに小さな数もあらわすことができるので、たいへん便利な記数法なのです。
ところで、「十一(じゅういち)」を書いてね、というと何も教わっていない子は「101」と書くのが普通です。お母さんたちはよく、「11は十が一で、一が一だから…」というような説明をされますが混乱しませんか?
そこで、数字の仕組みを理解するときに有効なのがタイルというわけです。タイルを使うと、「11」は下図のようにあらわせます。
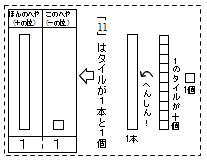
タイルのお家は個室制で、「こ」の部屋、「本」の部屋、「枚」の部屋があります。タイルが10こになると「本」の部屋に行かなければなりません。10こは1本のタイルと同じ大きさであることを確認し、1本のタイルに変身させます。タイルが1本と1こで「11」です。
タイルだと量の大きさをバックにして数字を勉強していけるのです。
実は、学校の算数の教科書では「0」より前に「10」を教えるものがあり、「10」を一つの数字と考えてしまう恐れがあります。
タイルの優れたところは、十あつまったときに一個のときとは違う形になって「1本」や「1枚」のようなかたまりを無理なく作れることです。丸いおはじきや計算棒では、箱に入れたりひもでしばったりしなければ、十をひとかたまりとしてあらわせません。
つぎの「三百四」という数もタイルであらわすと下のようになります。
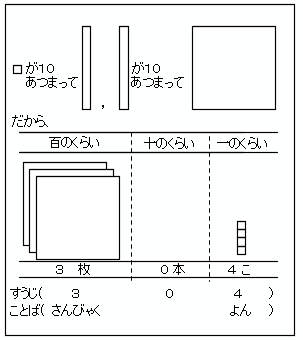
タイルであらわすと数の大きさがはっきりつかめます。
「三百四」→3枚0本4個 →「304」と並べて書き表します。
こうして位ごとに数字を並べて書く仕組みがわかれば、後に出てくるたしざんで「位をそろえて たす」ということも理解できます。くり上がりやくり下がりなど、計算の仕組みもタイルでバッチリ説明できるのです。
また、分数や小数、そして因数分解の考え方にもタイルが大活躍します。
5.順序を表す数
◎順番や位置をあらわす数(順序数)
ものの多さをあらわすのが「集合数」でしたね。
そして算数では集合数を数の基本と考えて教えます。集合数は自由にたしざんができます。
もう一つの数、「電車の1両目」とか「前から5番目」とか「3丁目6番地」といった順番や位置を表す数を「順序数」といいます。順序数は自由にたしざんができません。2等賞と3等賞をたしても5等賞にはなりません。
「順序数」は「集合数」を理解してから導入します。

〈かずの階段〉
1~9までのタイルを小さい順にならべさせます。小さい順に並べたとき、4のタイルは4番目にあり、4番目にあるタイルは4のタイルです。こうして集合数と順序数とが一つのものになっていきます。
ちなみに、英語では「集合数」と「順序数」を数詞の上でも明確に区別しています。
〈集合数〉 one,two,three,four,five,・・・・・
〈順序数〉 first,second,third,fourth,fifth,・・・・・
従来の算数教育は「数えること」、つまり「順序数」で“数”を導入していました。
《例》
1の次は2だから、1+1=2
2の次は3だから、2+1=3
3の次は4だから、3+1=4
…と「+1」が続く。
しかし、数えられるだけでは数はわかっていないということが明らかになり、今日ではほとんどの国が「集合数」で“数”を導入しています。
集合数を数の基本にして算数・数学教育を日本で初めて系統的にうちたてたのが「水道方式」による指導です。
集合数と順序数のちがいは意識して指導する必要があります。
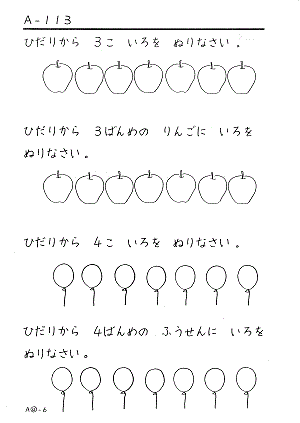
この二つが区別できているかな?と確認するために、こんな問題にも取り組みます。
数学で育ちあう会 A教材 A-113
いままでみてきたように、子どもが「数」を獲得するには大人の想像をはるかにこえて多くの過程をふんでいくことがわかります。
机に向かって鉛筆を持つだけが勉強ではありません。遊びや生活の中でさまざまな経験をし、「なぜ?」と問いかけ、友だちや家族とおしゃべりをする、そんなことが算数の世界をも広げていくのではないでしょうか。
とはいえ、今は学校に入学する前に算数の知識が入ってくることが当たり前になっています。それだけに、幼児のうちから算数ギライを生まないよう気をつけてあげたいですね。
こういった思いから、当会では幼児の算数指導を実践している教室もあります。おもに年中~年長の幼児さんや1年生になったばかりのお子さん対象に、数育会A教材をベースにして絵カルタ、カード、タイルなどを用いた数人のグループ学習を行い、時にはゲームを取り入れたりしながら楽しく学習しています。
「水道方式」の教材