のように「位の欠けているもの」から「答に 0 が入るもの」へと順に学習します。
「0+0=0に決まっているからこれ以上簡単なたし算はない」というのは大人の思い込み、子どもにはとても難しいのです。
0~9(または0~5)までの「数」がわかると、この範囲での たし算・ひき算 ができますね。
ところで、たし算 って どういうときにする(できる)でしょう?
次の①~⑩番の問題を ちょっと考えてみてください。
たせるかな? たせないかな?
① イヌ 3びき と ネコ 4ひき で なんびきですか?
② バナナ 3本 と エンピツ 2本 で なん本ですか?
③ きんぎょ 2ひき と さば 5ひき で なんびきですか?
④ 100円 と 500円 あわせて いくらですか?
⑤ 2m のひもと 5m のひもを つないだら なんmですか?
⑥ 鉄のパイプ 3本 と アルミのパイプ 5本 があります。パイプは あわせて なん本ですか?
⑦ 3リットルの水と0.2リットルの水をあわせるとなんデシリットルですか?
⑧ 石 3こ と 1円玉 5こ で いくらですか?
⑨ 1円玉 5こ と 50円玉 8こ で あわせていくらになりますか?
⑩ 5リットル の 水の中に 3m の ひもを入れるといくらになるでしょう?
いかがですか? 全問、素直に「たし算」ができましたか?
なんだか変…?? という問題も かなりありましたよね。
①は、「3+4=7 答 7ひき」とはしたものの、イヌとネコはたしていいのかな?…と迷います。
もし、「動物は あわせて なんびきですか?」と 問われていたらわかりやすいのに。
②は、「3+2=5 答 5本」と出したとしても、この「5本」とはいったい何の数なのでしょう…。「たしざん」を初めて習う子どもたちなら、もっと迷うにちがいありません。反対に、平気で「5本」と答えてしまう と、ほんとうにたし算がわかっているわけではないなぁと思ったほうが良さそうです。
子どもにたし算を教えるとき、「こんな方法もあるよ」「これもたし算なんだよ」とあれこれ一度に教えてしまうと頭の中 がゴチャゴチャになってしまいます。
はじめて習うところは、まず 基本の考えをしっかり定着させたい ものです。
例えば「3+2」とは何かを教える場合、まず最初は、
同じものどうしでたし算ができる
という ことを押さえます。
初めは具体物を使って実際にやってみせたり、子どもたちにも「たし算」の体験をさせてみてください。その場合、もし アメで教えようと思ったら包装紙も同じ色のアメにしましょう。
最初は厳密に同じものどうしにします。
あわせた数を出すのが たし算 です。
次のように、①→②→③→④の順番で、たし算を学んでいきます。
「お母さんの算数教室~たしざん・ひきざん」資料(田中恭子さん作)より

① では実際に2こと1このアメを「あわせる」操作をやってみせます。
② ではアメをタイルに置き換えてあわせてみせます。
③ ではたし算の式を教えます。式とは「さんすうの言葉であらわす」ことです。
④ ではたし算の意味を確認します。
ひき算 は、残った数を出す計算 です。
「アメが3こあります。2こ たべました。のこりのアメは なんこですか。」
このような問題からひき算を教えるとよいでしょう。最初にあった数から、[ たべたり、あげたり、つかったり、なくしたり、にげたり、帰ったり] していくつか取り除き、その残りを求める場合に ひき算を使います。
ひき算には他にもいろいろな意味があるのですが、上のような「残りを求める」(求算)ひき算が子どもたちに最もわかりやすく、操作がしやすいのです。
ひき算の場合も具体物から入って、タイル、式(さんすうの言葉であらわす)だけでできるようにしていきます。
常に「たし算(ひき算)ってどんな数を出すんだっけ?」と、たし算・ひき算の意味を聞いていくのがいいと思います。
子どもたちには、今、自分が何をしているのか、何を求めているのかをいつも意識してほしいですね。

あわせた数をだすのが「たし算」 で
残った数をだすのが「ひき算」 でしたね。
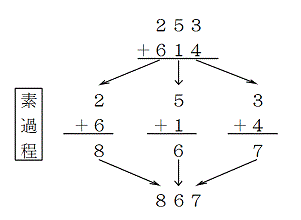
ところで、たし算はどんなにケタ数が多くなったとしても、「1ケタ+1ケタ」に分解することが出来ますね
このたし算の素になる 1ケタどうしのたしざん のことを たし算の素過程(そかてい)と呼んでいます。
たし算の素過程は、
0+0 から 9+9 まで 100個 あります。
これはたし算のおおもとのおおもとなので、1つも欠かすことなく教えなければいけません。
そして、たし算の素過程の逆が、
ひき算の素過程(そかてい)
になります。こちらも欠かさず教えていきます。
ではまず、たして 9までの「たし算」、つまり、くり上がりのないたし算 について、どんな順序で学ぶと良いかを考えてみましょう。
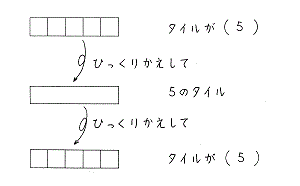
水道方式では、タイル□を使ってたし算を学習していきます。
タイル□は5個で「5」のタイルになります。「5」のタイルを使うことで5以上の数が一目でわかります。
たして9までのたし算(くり上がりなし)は、
①「5」のタイルを作るかどうか、と、
②「0」が含まれるかどうか、
で型分けし、次のような順序で教えると良いでしょう。
「お母さんの算数教室~たしざん・ひきざん」資料(田中恭子さん作)より

「お母さんの算数教室~たしざん・ひきざん」資料(田中恭子さん作)より

(キャタピラータイル)
私たちがふだん使っている数字は、「十進記数法(じっしんきすうほう)」といって、十集まれば次の位に一くり上がる仕組みです。「9」より1大きい数を1と0を並べて「10」と書くのもそのためです。これによって0~9までの十個の数字だけでどんなに大きな数もどんなに小さな数もあらわせるのでたいへん便利な記数法です。
10以上のものを数えるとき、10ずつまとまりにして数えていくと便利であることはみなさんも経験ずみですね。また「10」をつくるときに、例えば「6」と「4」の組み合わせや「7」と「3」の組み合わせというふうに、私たち大人はたやすく10をつくるためのペアを探し当てることができます。
子どもたちにはこの 「10」の合成・分解 が確実にできるように、タイルと数字で練習してもらいましょう。これが苦手だと、くり上がり・くり下がりの計算がスムーズにいきません。最後には、タイルがなくても数字だけですぐ答えられるくらいまでにしましょう。
↓作り方 と 使い方例 (田中恭子さんイラスト)

では「1ケタ+1ケタ」(素過程)のたし算で くり上がりのあるもの はどのように考えると良いでしょう。
「くり上がり」には、「10のかたまりを作る」 という作業が必要です。
タイルで考えると、「1本」のタイルをつくる ということになります。
※1個のタイル□が10個集まると「1本」のタイルになります。
数字の「10」はタイルが1本と0個という意味です。
タイルの仕組みについては こちら をどうぞ。
〈8+6〉 の場合(5・2進)
8 は 5 と 3
6 は 5 と 1
に分解できます。
タイルを置いて考えてみましょう。(下図)
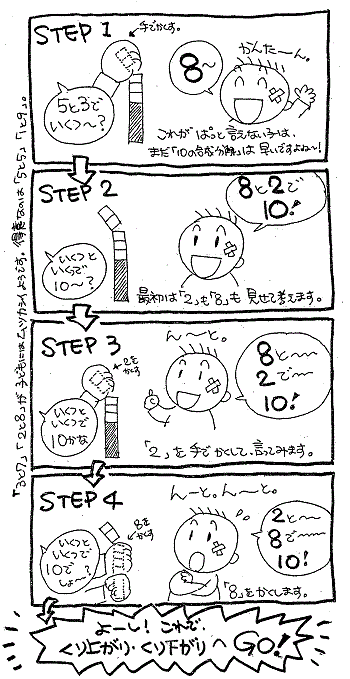
「10をつくる」➡「1本のタイルにへんしん!」➡「残りのバラタイルをあわせる」
”5と5で10♪(へんし~ん!) でっぱりどうし合わせて3と1で4♪ あわせて14”
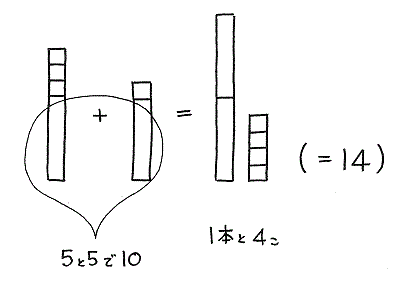
このように両方に5のタイルが含まれていると、5と5で10になるので簡単で理解しやすい方法です。
これと同じタイプは、9+5、7+7、8+7 ・・・ などがあります。
最初はこのタイプをタイルで操作しながら練習していくと10のかたまりを作ることが意識できて良いと思います。
〈9+4〉 の場合(補数繰り上がり)
9+4のように、一方が5より小さい場合は、5と5で10のかたまりが作れません。
この型では「9にいくつたすと10になるか(10の補数)」を考えさせて答えをだすほうが簡単ですね。
9と1で10が作れるので、4個のタイルから1個をもってくればすみます。
あとはバラタイルが残り、すぐに答えがでてきます。
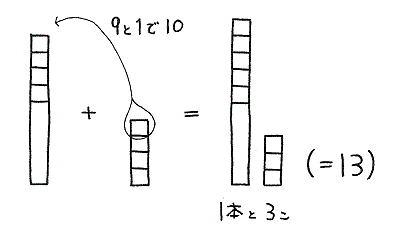
8+3、7+4 なども同じ補数繰り上がりタイプです。
タイルで正しい答えを確かめながら、やがてはたし算の式だけでも答えが出せるまで練習します。
たし算の素過程は確実にマスターさせましょう。
「10の合成」が確実にできていると、「8+6」のようなたし算も10の補数を考えるやり方で良いと思います。

いちばんぼし算数数学教室さん制作のYouTube『算数動画』
↓
くり下がりのひき算は、多くの子どもたちがつまずくところです。苦手なまま学年が上がればケタ数が増えてゆきづまってしまうので、素過程のくり下がりは確実にしておきましょう。
ではひき算の素過程で くり下がりのあるもの はどのように考えると良いでしょう。
「くり下がり」には、「10のかたまりをくずす」 という作業が必要です。
タイルで考えると、「1本」のタイルをバラバラにする ということになります。
〈13-9〉 の場合
13 は 1本のタイルと3個のバラタイルでできています。
一の位の 3 から 9 をひくことはできません。
そこで1本のタイルを10個にくずします。
10個(5のタイルが1つ+バラタイルが5個)から 9個をとり、
残り1個のタイルと3個とを合わせて答えがでてきます。
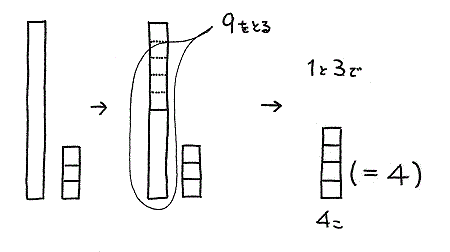
「10の分解」が身についていると、この方法でスムーズにくり下がりが理解できるでしょう。
タイルで正しい答えを確かめながら、やがてはひき算の式だけでも答えが出せるまで練習します。
ひき算の素過程も同じく確実にマスターさせましょう。
このようにくり上がり・くり下がりもタイルを使うと、計算の意味を考えながら計算力を習得できます。
たし算・ひき算の素過程(そかてい)は、算数学習にとって基礎中の基礎、これからの土台となっていくものなので、確実にしておきます。
最初は実物を使う、タイルを動かしてみる → タイルを置いてみる → タイルを書いてみる → タイル無しでやってみる、
というように少しずつ段階を上げてくり返し学習したいところです。
大事なところはていねいにじっくりと!
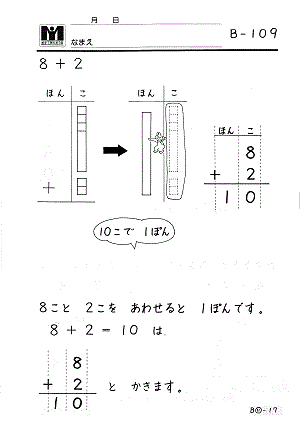
数学で育ちあう会 B教材 B-109
現在の小学校算数では、タテ書きの計算=「筆算」 が出てくるのは2年生からです。
でも私たちは、1ケタどうしのくり上がりやくり下がりが出てくる1年生から本来なら筆算を取り入れるべきだと考えます。
そのほうが数の仕組みに合っているからです。
教科書においても、数が大きくなれば筆算に切り替えざるをえません。位をそろえなければ、たし算・ひき算ができなくなってしまうからです。それならば早い段階から十進法を意識して筆算を導入してくほうがずっと良いのです。「水道方式」では、位をそろえて書く「筆算」を重視します。
ヨコ書き(暗算)の場合は、そろばんも同じなのですが上の位からたしていきます。筆算は数の仕組みにしたがって下の位から順にたしていきます。
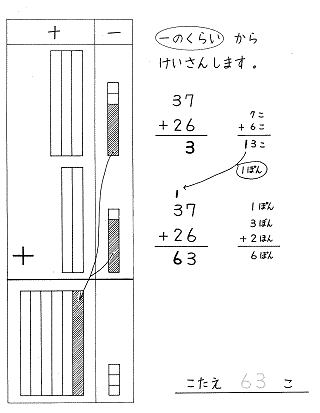
数学で育ちあう会 C教材 C-21より
〈ひき算〉
最初は2ケタ-2ケタでくり下がりが無い型(例:99-22)から導入し、各位どうしをひき算するという基本をおさえます。
それができてから、引く数に「0」が入るもの(例:99-20)、答えに0が入るもの(例:99-29)、位が欠けているもの(例:99-2)を扱います。
そして次に、くり下がりのあるひき算です。各位をそろえ、下の位から順にひき算をしていきます。
タイルでやってみましょう。
33-17
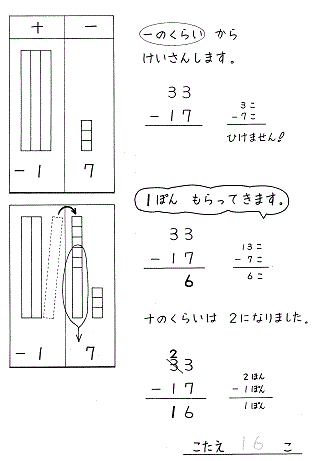
数学で育ちあう会 C教材 C-51より
水道方式では、すべての計算問題を 型分け し、「一般型」から「特殊型」へ という順序で教えていくのが大きな特徴です。
例えば3ケタのたし算は、教科書などでは、「500+200」のようなものを先に教えます。水道方式では、「123+455」のようなものを先にします。くり上がりがなく、全ての位に0でない数字がある。これを一般型として最初に導入します。
和が3ケタになるたし算は、おおざっぱに書くと次のような順序で学習します。
まず「一般型」をもってきて、各位どうしをたす ということをおさえます。

そして、それぞれの型の中で、例えば、エ.(2回くり上がり) ならば、
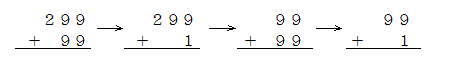
のように「位の欠けているもの」から「答に 0 が入るもの」へと順に学習します。
「0+0=0に決まっているからこれ以上簡単なたし算はない」というのは大人の思い込み、子どもにはとても難しいのです。
子どもたちは0という数字が出てくると途端にわからなくなりますが、3+5なら安心してたせますね。
一ケタどうしのたし算を、計算の最小のパーツで「素過程(そかてい)」といいました。
上のアの型の場合、素過程自体が簡単なので3ケタになっても簡単、それで一般型になったのです。
一般型ができればだんだん特殊な型へと流していきます。
ひき算についても同様に分類して、まずくり下がりがない一般型(例:999-222)から入っていきます。
このように型分けをしていると、苦手な型を取り出して練習できるのでとっても効率が良いのです。
3ケタ以上のたし算も各位をそろえ、下の位から順にたし算をしていきます。
タイルで考えれば計算の仕組みを目で確かめ納得できます。
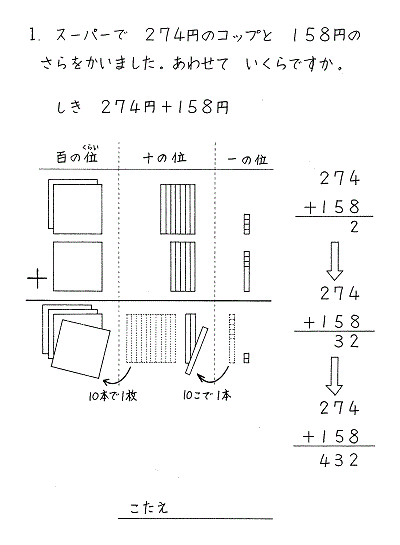
数学で育ちあう会 E教材 E-32より
..3ケタ以上のひき算も同じようにタイルで学習することで、各位をそろえて下の位から順にひき算をしていけば良いことが理解できます。
〈ひき算 の 間違い例〉
ひき算は苦手な子が多く、3ケタ、4ケタと増えれば、1問解くのに苦労します。子どもたちも大変しんどいところ。
ひき算で間違いの多い型が「401-123」や「300-167」のようなものです。
「ひけないので隣から借りようと思ったら0なので、そのまた隣から借りてくる」というパターンの問題です。
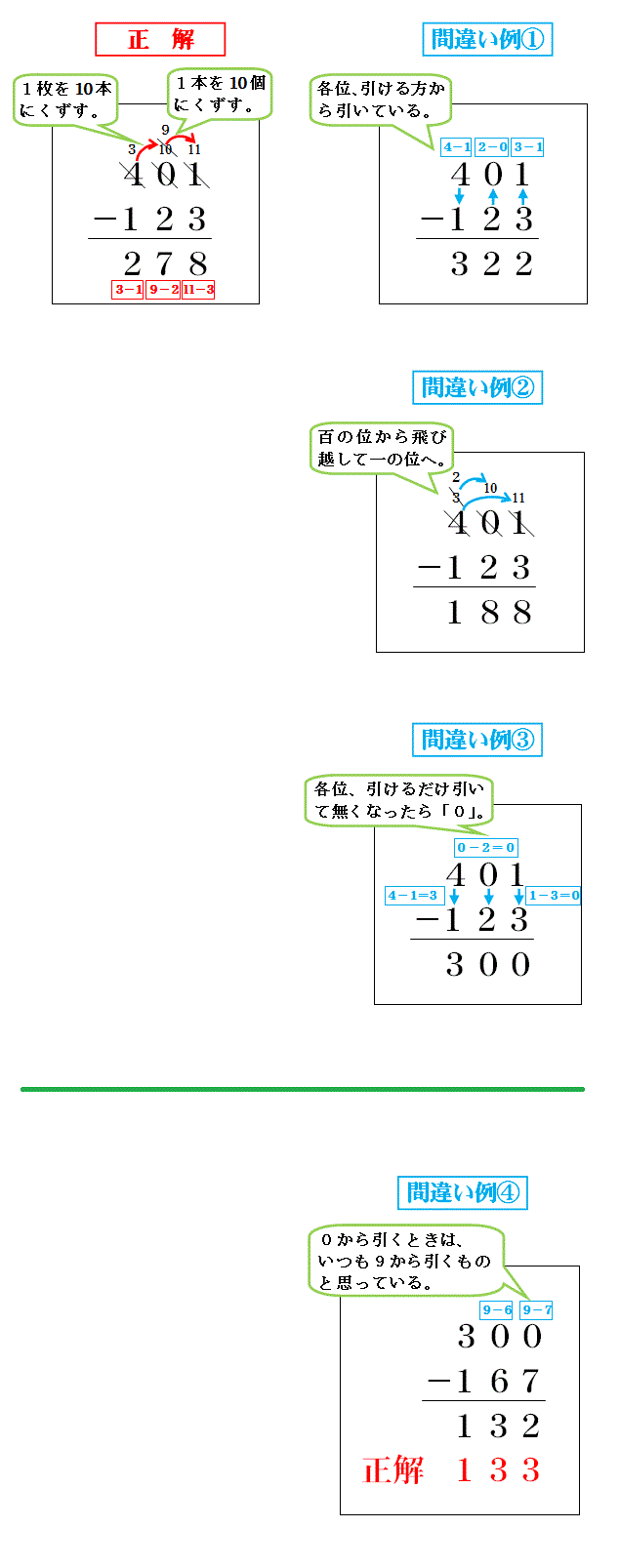
また、3ケタまでの計算はバッチリ!! と思っている子どもでも、4ケタのひき算で次のような間違いをすることがあります。
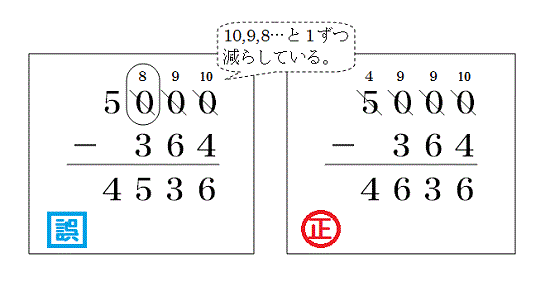
この考えだと、3ケタまでは間違わなかったはずです。でも実は、この子は数の仕組み(十進記数法)がわかっていなかったわけです。
この間違い例でもわかるように3ケタまでの計算では不十分です。4ケタの計算ができるとそれ以上の計算は同じようにできます。いっとき、「ゆとり教育」でなくなっていた4ケタの加減ですが、3ケタができているからといって4ケタも自然とできるわけではないことがわかります。

「いちばんぼし算数数学教室」さんのYouTube『算数動画』
よく、「計算はできるのに文章題が苦手で…」という話を聞きます。
問題を読んで正しい式が作れない子、文章題は苦手だとそっぽをむく子は大勢います。
たし算・ひき算 間違い例
①わなげをしました。
1かいめは 4つ、2かいめは 3つ はいりました。
あわせて いくつ はいりましたか。
しき 1+4+2+3=10
こたえ 10
②450円で
えほんをかって 500円 はらうと おつりはいくらですか。
しき 450-500=50
こたえ 50円
たし算・ひき算 の文章題は、大人にとってこれほど簡単なものはない! というふうに思えるのですが、まだまだ人生経験に乏しい子どもたちは ちょっとひねった問題になると 途端に混乱してしまいます。
上の間違い例のように、文中に出てきた数字を順番に書いて「+」か「-」でつないですませる場合も多いのです。
「問題をよく読まないからでしょ!」なんてつい責めてしまったり…。でも本当に、よく読めば解けるのでしょうか?
苦手の原因を、「読解力不足」と考える人もありますが、読書好きの子どもが得意かと言えばそうとも限りません。語彙(ごい)の貧弱さ、イメージ力の乏しさもあるけれど、主要な原因は、「演算の意味」がしっかり教えられていない ことにあります。また「量」になじんでいないこと、たしざん・ひきざんができる量かどうかの区別の指導が軽く扱われていること も影響しています。
これまで何度もお話ししてきましたが、最初に演算を学ぶ上で大切なのは、どんな時に使う計算か、その意味をわかっているかどうか ということです。おさらいをしますと、
あわせた数を出すのが 「たし算」 で、
残った数を出すのが 「ひき算」 でした。
これが最も基本となる考え方になります。
この基本の考え方で、一番典型的な場面を例にして、たし算、ひき算とはどういうものかを学び、計算を習熟した後、
いろいろな種類の問題を指導していきます。
実はたし算・ひき算はいろいろな型に分類することができます。教える側の大人は、そのことを知った上で子どもの状況に合わせた与え方をする必要があります。
〈たし算の種類〉
たし算の基本は「あわせていくつ?」なので、最初は次のような問題で考えます。

本物のみかんを手に持って目の前のお皿にバサッと入れてみます。小さい子どもたちは実物やタイルを動かす操作活動を通して思考力が育ちます。最初に「合併型」を持ってくるのは、操作をしやすく子どもたちに理解しやすい からです。
続いて、同じ「あわせていくつ?」になるのですが、違う種類のものをあわせています。

男の子3人と女の子1人で何人か?といった問題に「男の子と女の子はたせない」とひっかかる子どももいます。子どもは全部で何人かと聞くことで納得できるでしょう。
次は、時間的経過を伴うたし算です。

体重が増えた、赤ちゃんが生まれて人口が増えた、といった場面もこの型になります。
合併型の①と②は、たす順番を変えても成り立ちますが、③の場合は成り立ちません。
これらが1~2年生でおもに扱われるたし算です。
このほかに、一方より多い量を求める場合のたし算もあります。

この場合は、シールが増えたわけではありません。兄の分は、弟の数を兄の数に置き直して3を加えることで出てくるので、一段階、難しくなります。
また、弟が5枚、兄は8枚なので、シールの数は全部で13枚存在していますね。
ここまでは、ものの多さを表す数(集合数)どうしのたし算でした。
今度は、○番目 のような順番とか位置を表す数である「順序数」のたし算になります。 順序数は、例えば1等と3等をあわせても4等にならないように、いつでもたし算ができる数ではありません。
けれど、次のような例ではたし算で答を求めることになります。

順序数はいつでもたし算ができるわけではないので注意が必要です。
このタイプはたし算の学習のずっと後の方で学ぶのが良いと思います。
このように、一口にたし算といってもいろいろな種類があることがわかりますね。
けれど、あらゆるたし算は「あわせていくつ?」という合併型にもどして説明することができるので、
「合併」をたし算の基本と位置づけているわけです。
〈ひき算の種類〉
ひき算の基本は「のこりはいくつ?」なので、最初は次のような問題で考えます。

ひき算においては、実物やタイルを動かす操作活動がしやすい「除去」が最もわかりやすい例です。 取り除いた残りを尋ねているので、ひき算のイメージに合っています。
続いて、求残に近いけれども実際に減ったわけではないという場合です。

たし算②の逆にあたります。
上の二つはさほど難しくありませんが、次の差を求めるものは一段と難しくなります。

「女の子から男の子はひけない…」とひっかかる子どもがいます。
この場合は、女の子と男の子に手をつながせて1対1対応させます。すると、手をつなげなかった女の子が出てくるので女の子の方が多いとわかります。「女の子全員」から、「男の子と手をつないだ女の子」をひいて「残りの女の子の数」が出てきます。「のこりはいくつ?」のひき算の意味にも合うわけです。
こうしたていねいな指導が必要なので①と②のタイプが十分できるようになったずっと後に③の求差型を入れるべきです。けれど教科書では求残型のすぐ後に差を求めるひき算が出てくるので混乱の原因になっています。

比べるものが異なる種類になると更に難しくなります。こたえの助数詞にも注意が必要です。
このほかに、たし算④に対応して、一方より少ない量を求める場合のひき算もあります。

この場合も、シールは減りません。二つの量の「差」がわかっていることになります。
そしてやはり弟が5枚、兄は8枚なので、シールの数は全部で13枚存在していますね。
ひき算の場合も、次のような例では「順序数」のひき算で答を求めることになります。

順序数はいつでもひき算ができるわけではないので注意が必要です。
このタイプはひき算の学習のずっと後の方で学ぶのが良いと思います。
このように、ひき算の種類もさまざまです。
けれどやはり、ひき算の基本は、「のこりはいくつ?」という求残型であると言えます。
「文章題」で大切なのは、
何と何がわかっていて、
何を求めるときにどんな式をたてるのか
です。
たし算・ひき算を初めて学ぶ子どもたちに対しては、できるだけ具体物とかタイルを使ってくり返し操作(合併と除去)し、経験させます。そしてそれらを、さんすうの言葉でどう表すのか を、折にふれ示していくと、文章題はできるようになります。
はじめて習うところは、まず、 基本の考えをしっかり定着させる ことが大切です。それは後ほど習う「かけ算」「わり算」についても同じです。
ところで、よく文章題を教えるときに、「もらった」「多い」などの言葉があればたしざん、「食べた」「帰った」などはひき算、などと教えている人を見かけますがどうでしょう? 次の問題を考えてみてください。

「もらった」や「ぜんぶで」など、たし算を連想させる言葉が入っていますが、求める式はひき算になります。それに問題のお話が最初に持っていたみかんより増えているので、「たし算」と勘違いする子どもは多いのです。「3+7=10」としたり「4+3=7」とする間違いがよく見られる問題で、一般には「逆思考」問題とも呼ばれています。

今度は「出ていった」の言葉が入っていますが、求める式はたし算になりました。そしてお話の内容では車の数がはじめより減っているので、たし算で求めることに違和感を覚える子どもも多いのです。「出ていった3台に駐車場へ帰ってきてもらうとどうなるかな?」と言って元の状態に戻してみたら気がついてくれます。
大人と違い、子どもたちはちょっとしたところでひっかかりを抱いてわからなくなっている場合があります。どこがわからないかと聞いても、低学年の子どもはうまく言葉で説明できません。具体物や絵で説明したり、ストーリーを追ってわかっていることを一緒に確認したり、数字を易しいものに変えて考えさせたり、どこでひっかかりを持っているかを見つけてあげて、教える側が適切な助言をすることでわかってくれることもあります。
いままで見てきたように、1年~2年生くらいでいろいろなタイプの問題が出てきますので、子どもの発達段階によっては途方もなく難しくなる ということをどうか知っておいて下さい。文章題の力をつけようと買ったドリルで子どもが混乱して自信をなくすケースは意外と多いので気をつけてあげましょう。
文章題を解く力をつけるために、式を与えてその式になる文章題を子どもたちに作らせることがあります。「問題作り(算数のお話作り)」と呼んでいて、基本的な演算の意味がわかっているかどうか確かめる時には有効です。
けれども次のような例もみられます。

これは極端な例ではありますが、子どもたちの中には、現実の世界ではあり得ない数値を設定してしまったり、たし算できないもの、たし算しても意味がないものをたしてみたりということがしばしば見られます。たとえ計算の答が正しく導き出せたとしても、たし算・ひき算がわかっているとは言えません。量や単位の感覚が現実とかけ離れている子ども、生活の中で量や単位にふれあえていない子どもたちが多いように思います。
計算が正しく早くできても、それだけでは役に立ちません。計算なら電卓の方がよほど早くて正確です。算数が役に立つためには文章題が解けることが大事です。文章題は身の周りの問題を数学的に解決するものだから、生活経験や遊びから学び取るものが大きい のです。
大いに遊び、そして量の世界とも親しみ、感覚を養って算数に強くなりましょう。
いつもは子どもに「問題をちゃんと読んだらわかるでしょ!」なんて言っているけど、
文章題ってやっぱり、面倒で た~いへん!
簡単! 楽勝!…なんて思っているお父さん、お母さん、
子どもの気持ちになって、大人も、たし算・ひき算に取り組んでみませんか。
こんな問題、やってみよう!(これは大人向け問題です。小さい子どもさんにさせて困らせないでね!)
① 校内マラソンで私は49位、正さんは27位でした。
正さんがゴールしてから私がゴールするまでの間、何人の人がゴールしましたか?
② 超大作映画を見に行きました。
映画は、午前10時50分に始まって、3時間20分かかります。
おわるのは、午後何時何分ですか?
③ 1秒間あたり10mの速さで走る電車と、1秒間あたり15mの速さで走る電車をつなぐと、
1秒間あたり 10+15=25m の速さで走る電車になりますか?
④ 1分間あたり40mの速さと、1分間あたり60mの速さをたして、速さが100m/分になることがあるで
しょうか?
⑤ 40℃のお湯に50℃のお湯を加えると、40+50=90℃ のお湯になりますか?
⑥ 今年の10月1日の北九州市の最高気温は18℃で、去年の同日の最高気温は16℃でした。あわせると何℃ですか?
また、この問いに意味があるでしょうか?
⑦ 9℃+12℃=21℃ が成り立つような文章題を考えて下さい。
⑧ 全商品30%引きと書いてある店で、2つの商品を買うと30+30=60%引きになりますか?
⑨ 体重が32㎏の男の子がいます。二つのヘルスメーターを並べて置き、二つに片足をのせて上がり、ピタッと
止まったときにそれぞれのメモリをよみました。すると、右のヘルスメーターは19kgを指していました。
このとき、左のヘルスメーターは、32-19=13㎏ を指すでしょうか?
⑩ 500gの水の中に100gの砂糖を入れて溶かしました。
全部で何gになりますか?
また、500gの水に100gの木を浮かべました。全部で何gになりますか?
今度は、500gの水に100gの氷を浮かべました。溶ける前と溶けた後で
それぞれ何gになるでしょう?
⑪ 油の量は重さ(g)で表示してあるのに、しょうゆや牛乳は体積(mLやL)で表示してあります。なぜでしょう?
【解答解説】

時刻に時間をたす問題です。時間の計算では単位をそろえることが大切です。60分でくり上がるので難しいですね。おまけに、午後何時何分かと聞いているので答えの書き方には注意が必要です。

③ 速さは自由にたし算・ひき算ができない量です。この場合はたし算は成立しません。
④ 速さのたし算が成り立つ例です。他に、川の流れと船の速度などで出題されるケースもあります。

⑤ 温度も自由にたし算・ひき算ができない量の一つです。皆さんも経験して知っている通り、この場合のたし算は成立しません。
⑥ 気温も同じく自由にたし算・ひき算はできませんが、平均気温などを出す場合の過程でたし算をする意味はありますね。
⑦ 気温に温度差をたす問題の例です。

⑧ もしこんなたし算が成立したら、商品が無料になったり、逆にお金をもらえてしまうこともありえますね! 2つの商品を買ったとき、a円の30%引き と b円の30%引きになるので、合計金額(a+b)円の30%引き になります。

⑨ 「重さ」という量は目で見ただけではわかりずらいですね。それゆえ、自由にたし算・ひき算ができると考えられない子は多いです。実際に体重計でこのような実験をしてみるといいかもしれません。
⑩ こちらも全て重さは600gになります。砂糖が水の中に溶けて見えなくなってしまうと「重さ」までなくなったと考える子どもは案外多いのです。浮かんでいる木も、水中を動いている魚も重さはちゃんと存在しているので、たし算が成り立ちます。「重さ」には「加法性」があることを子どもたちには知ってほしいと思います。ちなみに「かさ」(体積)はというと、「1リットル+1リットル=2リットル」にならない場合があります。
⑪ 同じ油の重さでも、夏と冬とでは体積が変わるので、油はグラム表記になっています。ご家庭で、油の重さ表示と、ジュースなどの表示を見比べてみましょう。こういった身近なものの表示を調べてみると、子どもたちにも量感覚や単位の感覚が育ちやすいのではないかと思います。
いずれも、生活経験が重要 ということです。